Алгебра - один из ключевых разделов математики, но многие ученики сталкиваются с трудностями при решении задач. В этой статье разберём пошаговые методы, типовые ошибки и полезные советы, которые помогут вам освоить алгебру и повысить успеваемость.
Основные этапы решения алгебраических задач
Любая задача по алгебре требует системного подхода. Вот универсальный алгоритм:
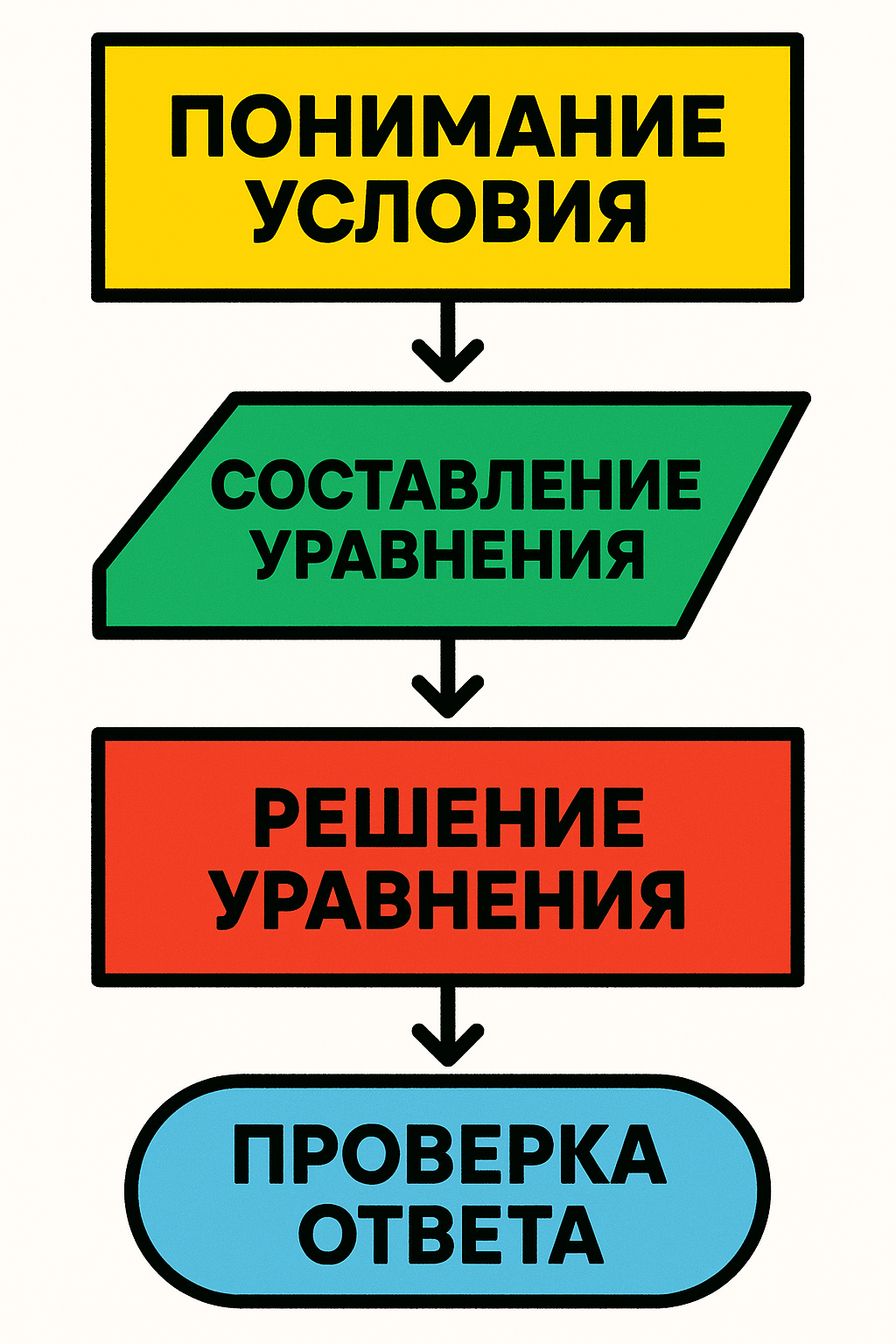
- Анализ условия - выделите известные и неизвестные величины.
- Выбор метода - определите, какие формулы или теоремы применимы.
- Составление уравнения - преобразуйте условие в математическую модель.
- Решение уравнения - найдите корни или искомые значения.
- Проверка результата - подставьте ответ в исходное условие.
Пример решения задачи
Задача: Найдите корни квадратного уравнения x² - 5x + 6 = 0.
Решение:
- Определяем коэффициенты: a = 1, b = -5, c = 6.
- Вычисляем дискриминант: D = b² - 4ac = 25 - 24 = 1.
- Находим корни: x₁ = (5 + √1)/2 = 3, x₂ = (5 - √1)/2 = 2.

Типовые ошибки и как их избежать
| Ошибка | Как исправить |
|---|---|
| Неправильное применение формул | Повторите основные формулы и их вывод |
| Арифметические просчёты | Проверяйте вычисления на каждом этапе |
| Неверная интерпретация условия | Выделяйте ключевые данные в задаче |
Советы эксперта для эффективного обучения
- ✅ Начинайте с простых задач, постепенно увеличивая сложность
- ✅ Решайте задания разных типов для лучшего понимания
- ✅ Разбирайте ошибки - это ключ к улучшению результатов
- ✅ Используйте графики для визуализации уравнений
Когда нужна помощь репетитора?
Если самостоятельное изучение даётся сложно, профессиональный репетитор поможет:
- ✅ Объяснить сложные темы простым языком
- ✅ Составить индивидуальный план обучения
- ✅ Научиться решать задачи без стресса
- ✅ Подготовиться к экзаменам и контрольным

Популярные вопросы
Какие темы по алгебре чаще всего вызывают сложности у учеников?
Мы помогаем разобрать каждую тему шаг за шагом, используя понятные примеры и практические задания. Наши методики позволяют закрепить материал и научиться применять его в любых задачах.
Как проходит индивидуальное занятие по решению задач по алгебре?
Мы используем
интерактивные материалы
и визуализацию, чтобы сделать обучение наглядным. Преподаватель адаптирует темп под уровень ученика, уделяя внимание «слабым» местам.Можно ли подготовиться к ОГЭ или ЕГЭ по алгебре за короткий срок?
Мы разрабатываем персональный план с упором на задачи из экзамена. Например, за 3 месяца реально подтянуть алгебру с «тройки» до «пятерки», если следовать нашей системе.
Как научиться решать текстовые задачи по алгебре?
Мы учим не просто «подставлять цифры», а мыслить структурно. Для тренировки разбираем задачи из реальной жизни — это повышает интерес и понимание.
Почему важно изучать алгебру, даже если она кажется сложной?
Наши занятия показывают, как алгебра применяется в науке и IT. Например, уравнения используются в физике, а графики — в экономике. Мы делаем акцент на практическую пользу, чтобы мотивировать учеников.
Как объясняются сложные темы, например, логарифмы?
Каждое правило подкрепляется
практическими упражнениями
с постепенным усложнением. Ученик получает чек-листы для запоминания свойств логарифмов.Что делать, если пропустил много тем и не знаешь, с чего начать?
Пример: если ученик не понимает квадратные уравнения, возвращаемся к линейным. Такой подход устраняет «белые пятна» и дает уверенность.
Как родители могут отслеживать прогресс?
Родители видят, как растет скорость решения задач и уменьшается количество ошибок. Можно подключиться к итоговому уроку, чтобы услышать выводы преподавателя.
Есть ли гарантия, что после занятий я смогу решать задачи самостоятельно?
К концу курса ученик:
Для уверенности проводим
«экзамен»
на последнем занятии.